
Zadanie Sumy i różnice (sir)
Pomóż nam usprawnić bazę zadań!
Sumy i różnice
Limit pamięci: 32 MB
Mamy dane  liczb całkowitych. Zastanawiamy się, ile jest uporządkowanych
par liczb
liczb całkowitych. Zastanawiamy się, ile jest uporządkowanych
par liczb  i
i  , w których zachodzi warunek:
, w których zachodzi warunek:  .
.
Wejście
W pierwszym wierszu wejścia znajduje się jedna liczba całkowita
 (
(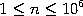 ). W kolejnym wierszu znajduje się
). W kolejnym wierszu znajduje się  liczb
całkowitych
liczb
całkowitych 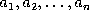 (
(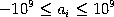 ),
gdzie
),
gdzie  oznacza wartość
oznacza wartość  -tej liczby.
-tej liczby.
W testach wartych około  punktów zachodzi dodatkowy warunek:
punktów zachodzi dodatkowy warunek:  .
.
Wyjście
W pierwszym i jedynym wierszu wyjścia powinna się znaleźć jedna liczba całkowita, równa liczbie uporządkowanych par, których różnica jest większa od sumy.
Przykład
Dla danych wejściowych:
3 -1 2 3
poprawną odpowiedzią jest:
2
Wyjaśnienie do przykładu: Wszystkie pary to:  .
Dwie pary spełniają zadany warunek:
.
Dwie pary spełniają zadany warunek: 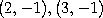 .
.
Autor zadania: Jacek Tomasiewicz.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English